Henry Eugene Vandervell ends The Figure Skate with a challenge: to skate a hypocycloid.
The hypocycloid is the most difficult of three curves he describes: the epicycloid, the cycloid, and the hypocycloid. All three are the designs made by a point on the edge of a circle being rolled along a line. For the epicycloid, the line is curved and the circle rolls along the outside. For the cycloid, it’s straight. For the hypocycloid, it’s curved and the circle rolls along the inside.
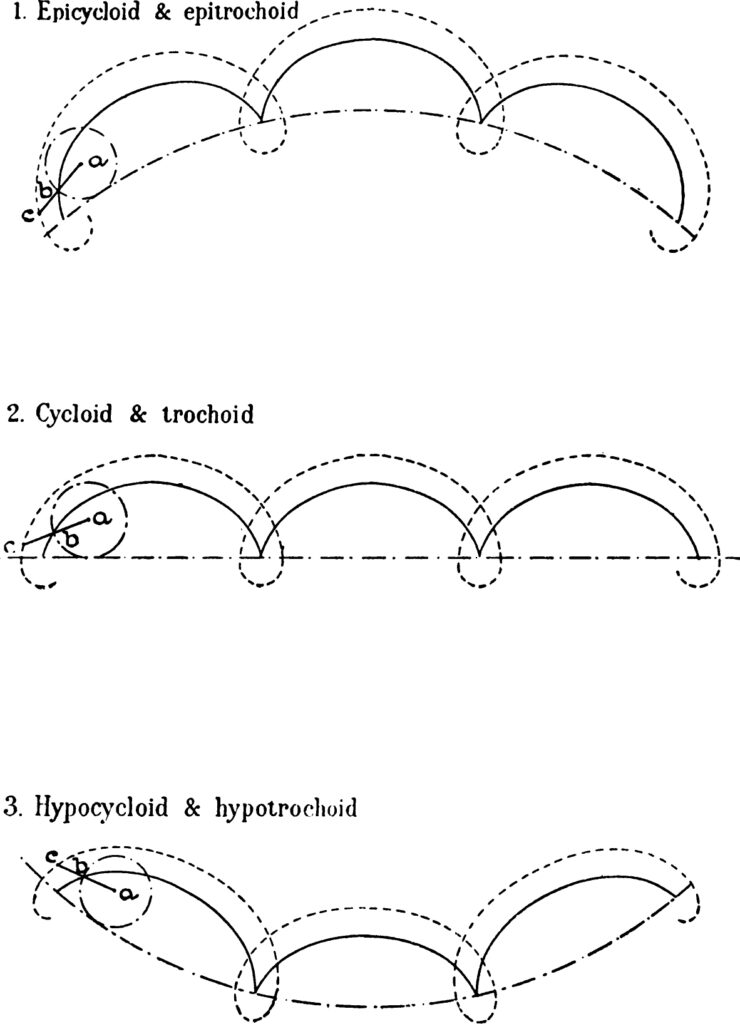
The first of these is simply the double three known in compulsory figures and on the juvenile and intermediate moves tests. The second two are more challenging. Vandervell concludes with a section called “The paradox”:
The way to attempt this figure is to start with the intention of making, say two turns and three curves (none less will show it), but to endeavour to make the contour of the group a straight line, instead of curved as in the epicycloid.
If this is done cycloid curves will be the result. This may be called the first stage, and no further progress can possibly be made until it is attained.
Vandervell 2020, 77
Here’s what I managed:
The first stage being accomplished, and proceeding on the same principles, the skater must now start again, and endeavour to bend or curve the contour of the group of turns past and beyond that of the cycloid, until such contour becomes outwards, and thus exactly the reverse of the epicycloid.
If this can be done the paradox will be resolved.
Vandervell 2020, 77
And here it is done, more or less:
Reference
H. E. Vandervell. 2020. The Figure Skate: A Research into the Form of Blade Best Adapted to Curvilinear Skating. Edited by B. A. Thurber. Evanston, IL: Skating History Press. First published 1901.
